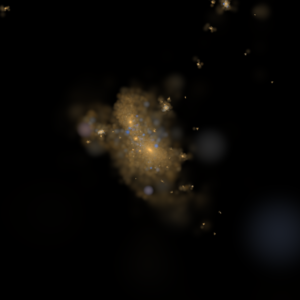
TangoSIDM Galaxy Catalogue
Ensemble of 3 Mpc regions taken from the TangoSIDM hydrodynamical cosmological simulations centered in the most massive galaxies. The regions are shown in pairs of dark matter (left) and stars (right). The panels showing the stellar component of the simulations correspond to gri-composite color images.
Dark Matter
Stars
Dark Matter
Stars
Dark Matter
Stars























Videos
Examples of analysis in particle collisions and dark matter halo evolution made during the generation of the TangoSIDM simulations.
Two particles collision test
In this simple example we test our algorithm in the collision of two particles. Do we conserve momentum and energy? Do we control the probability of collision? These are questioned that we thought about when doing the test.
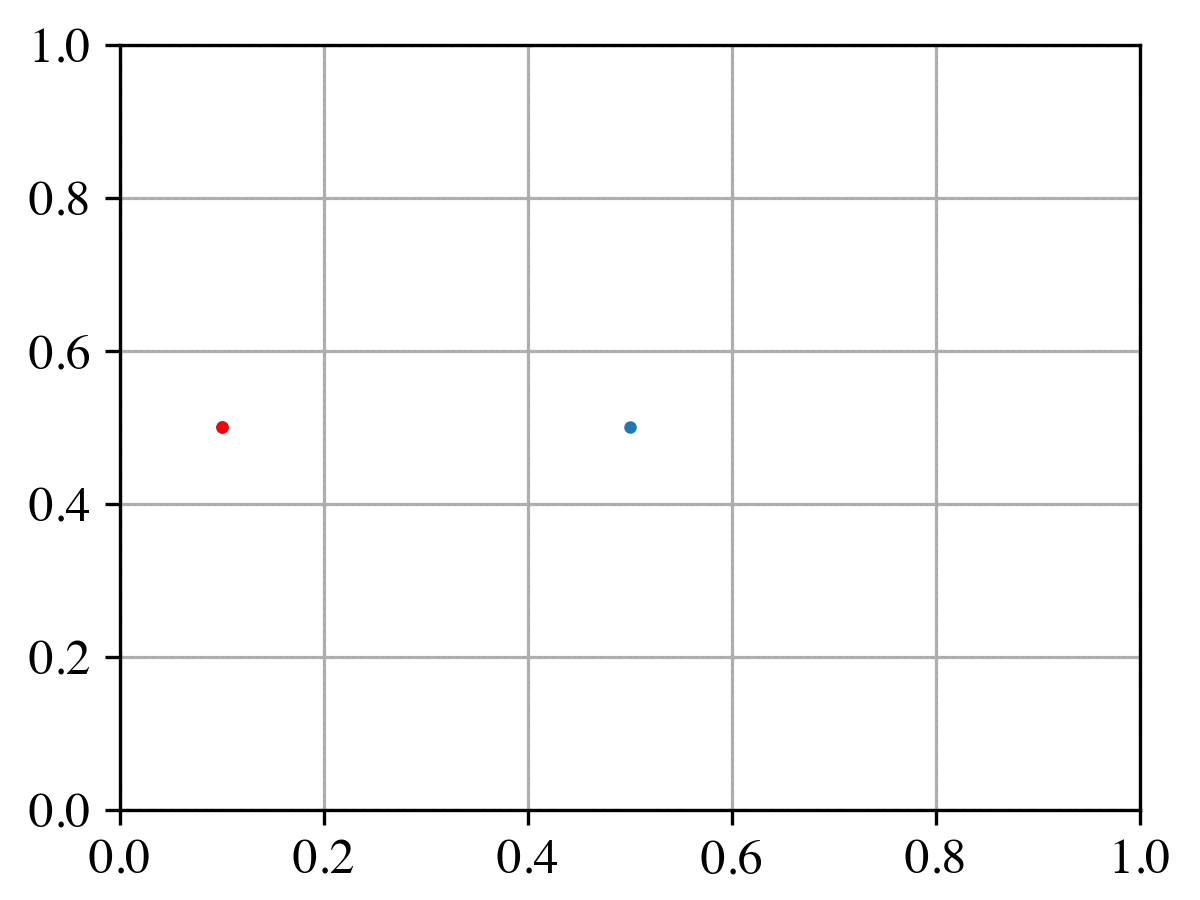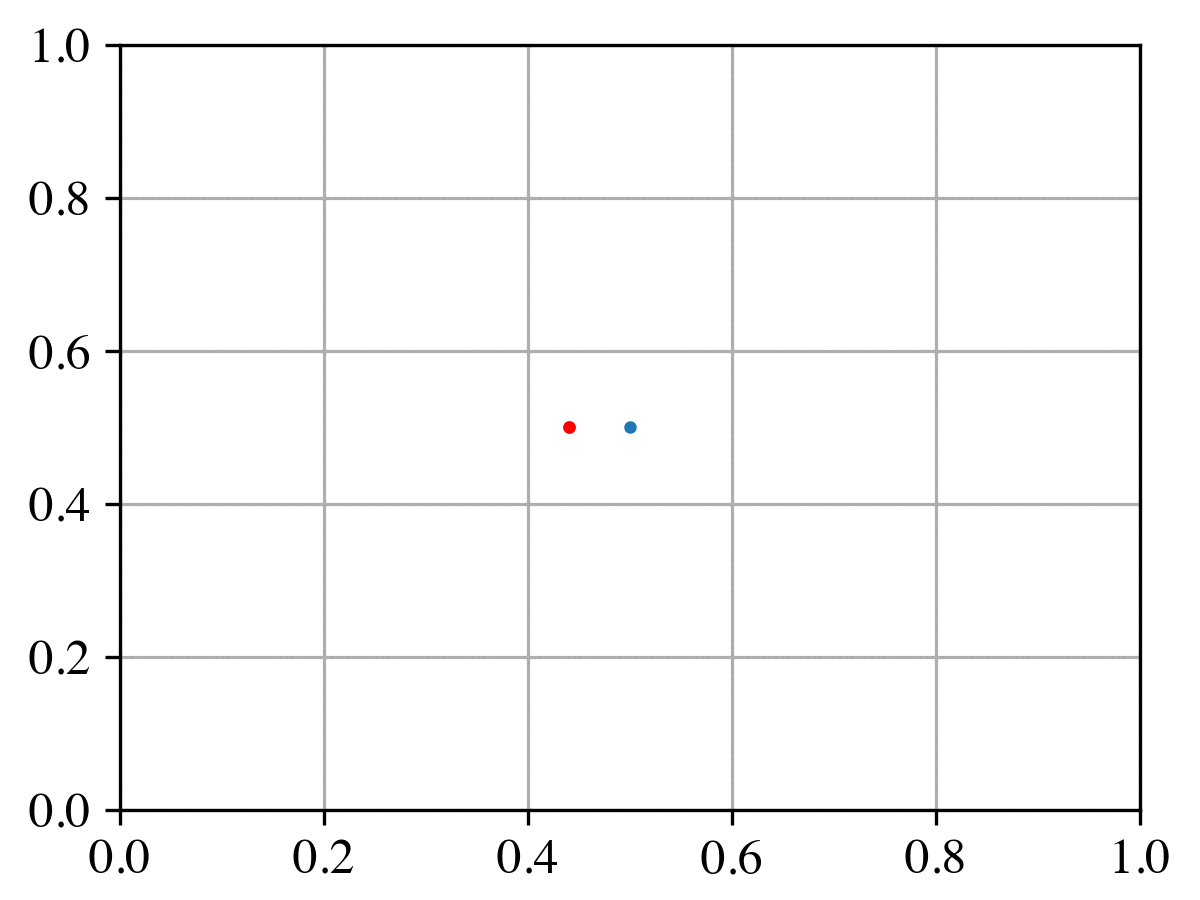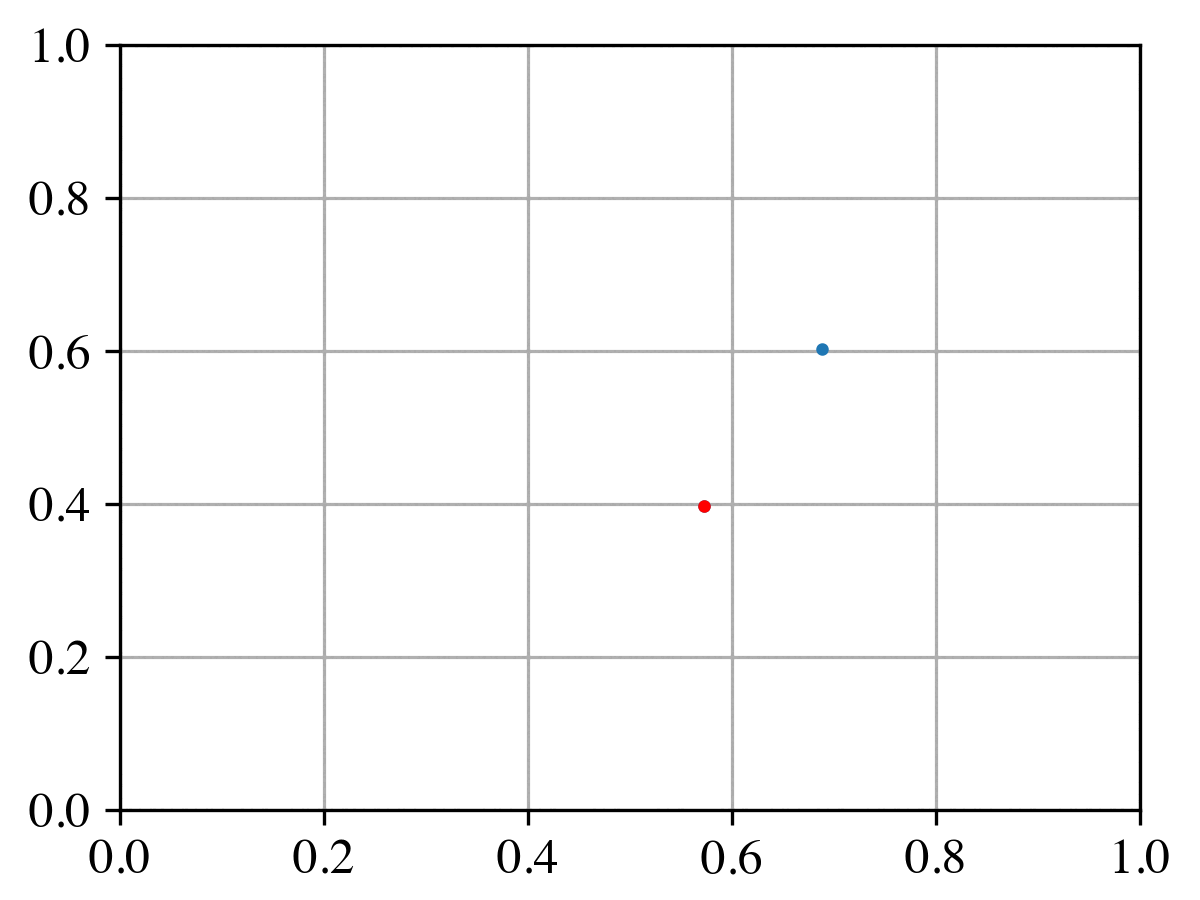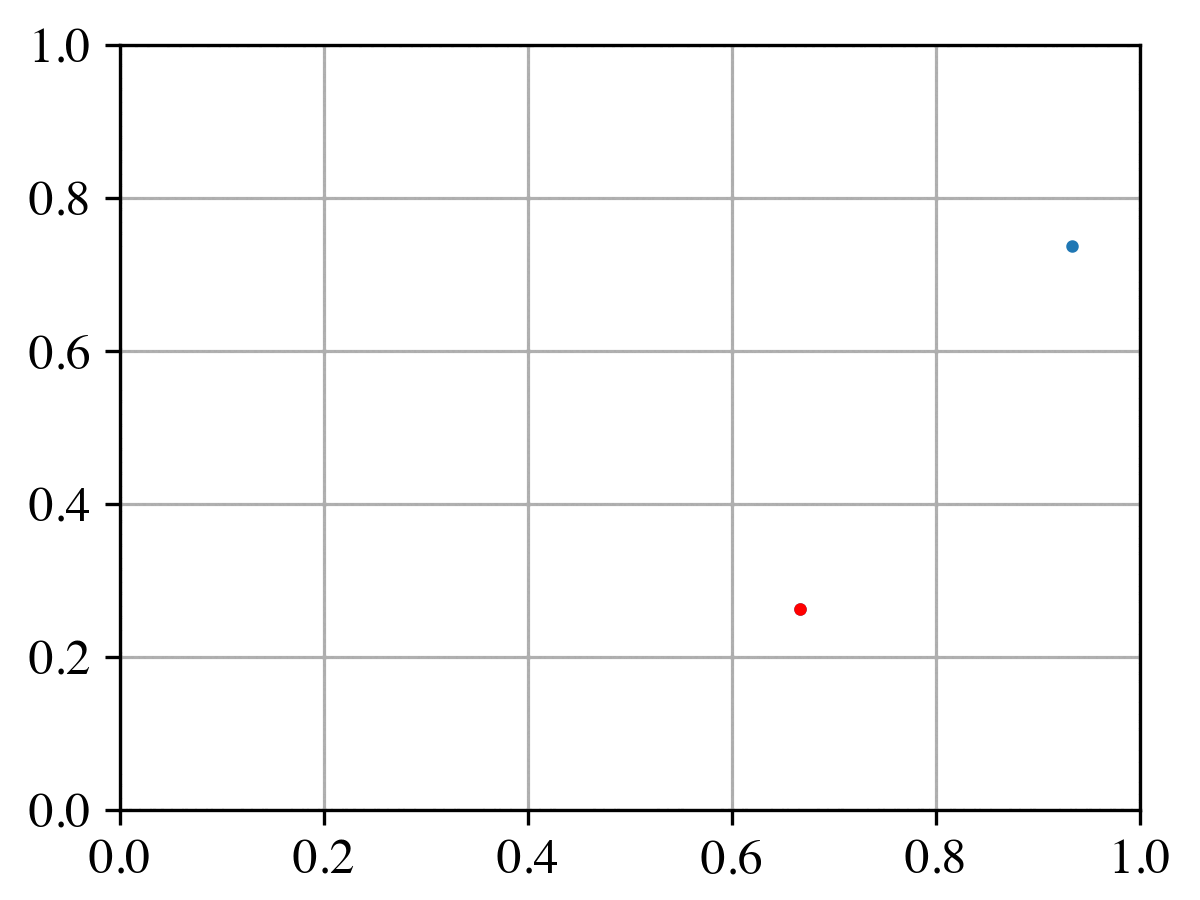
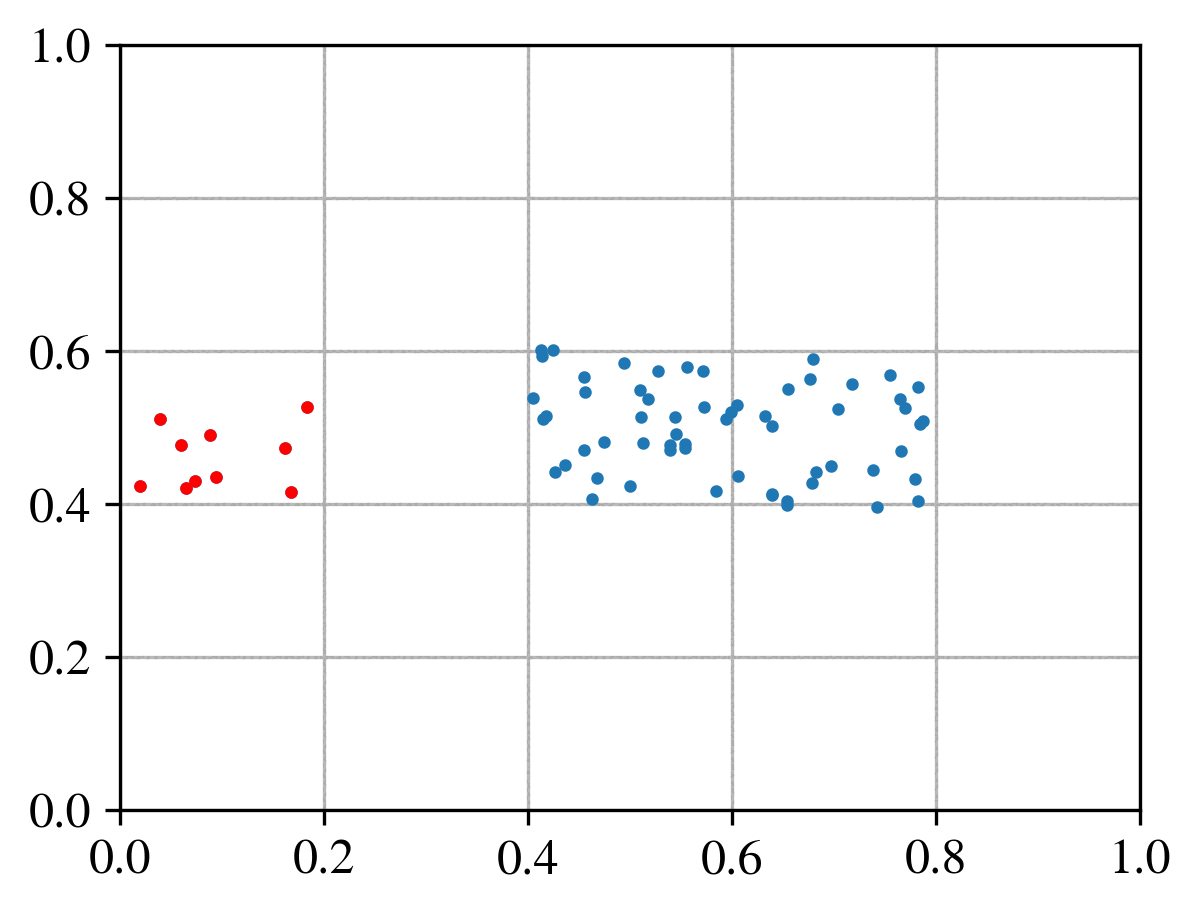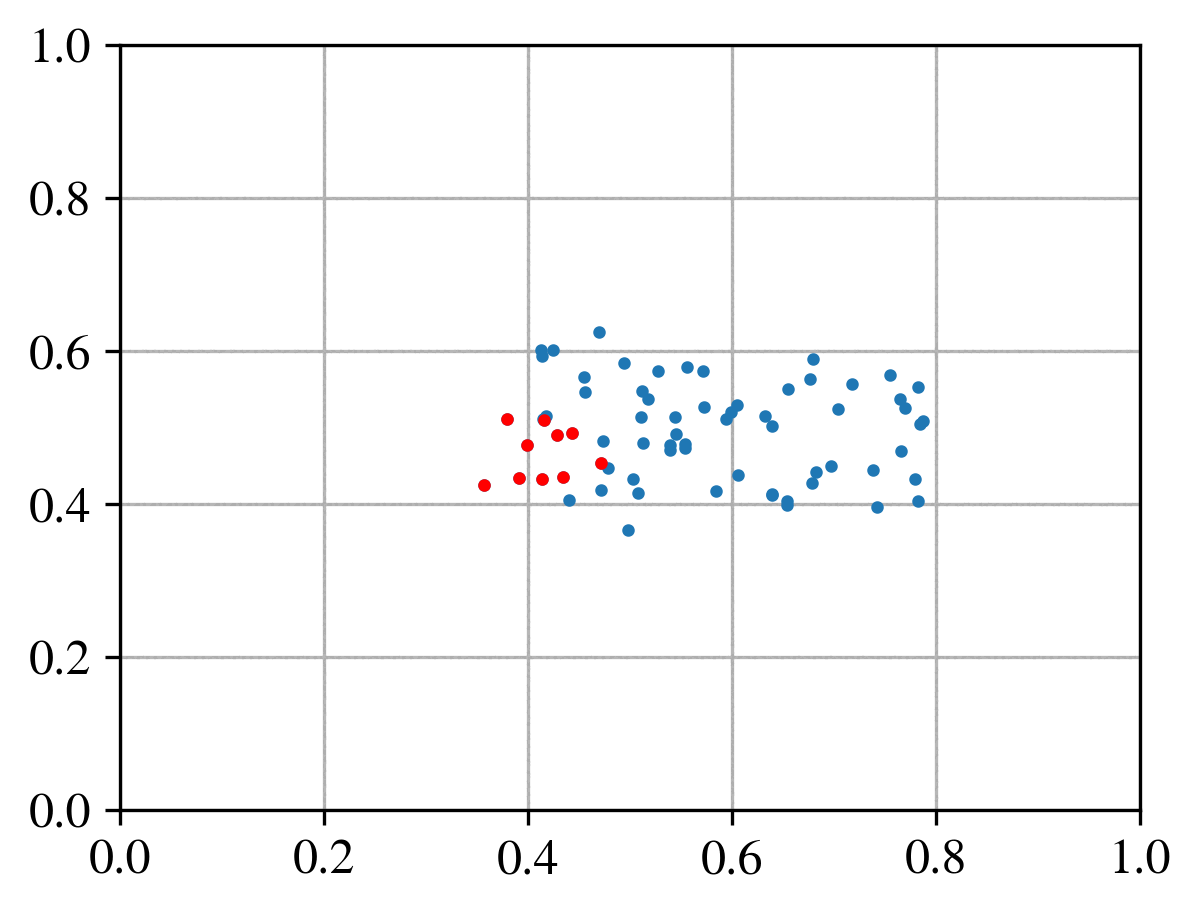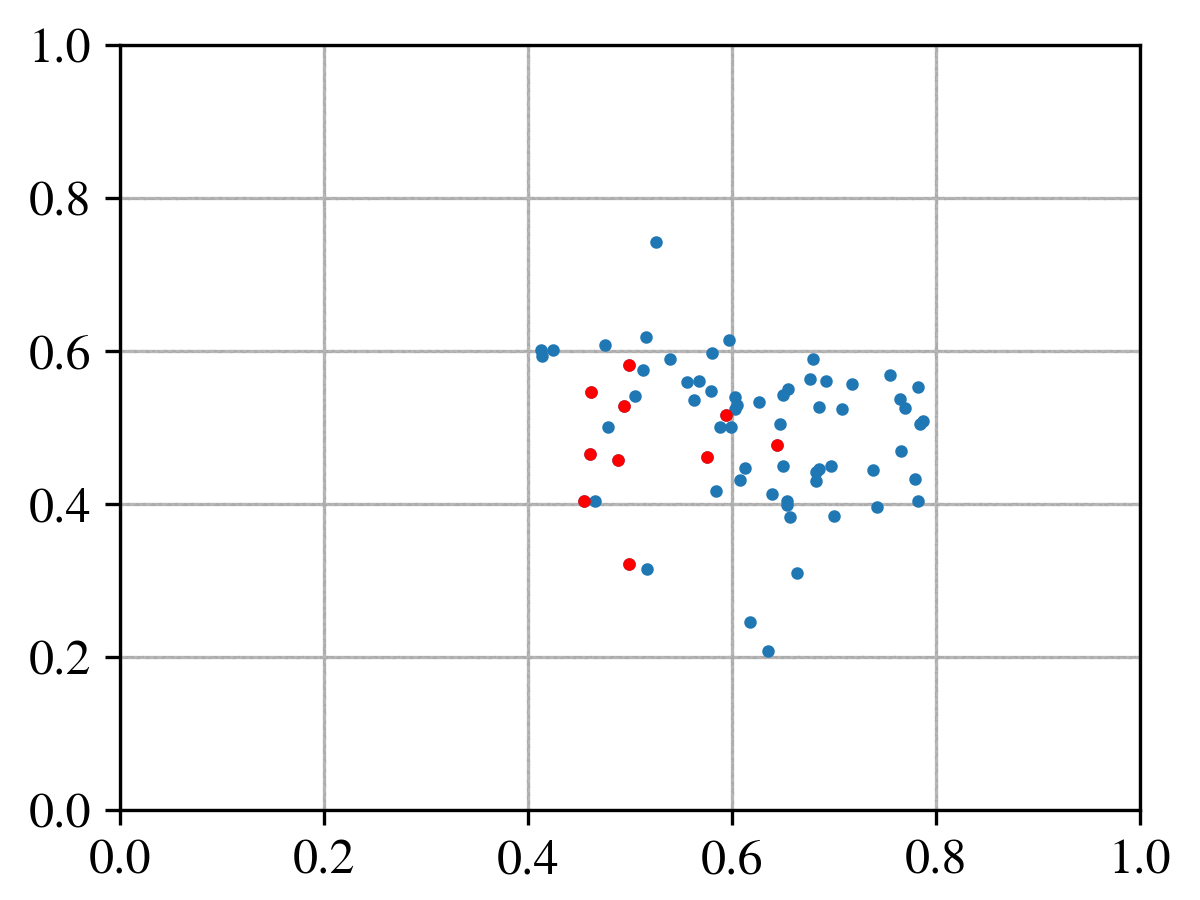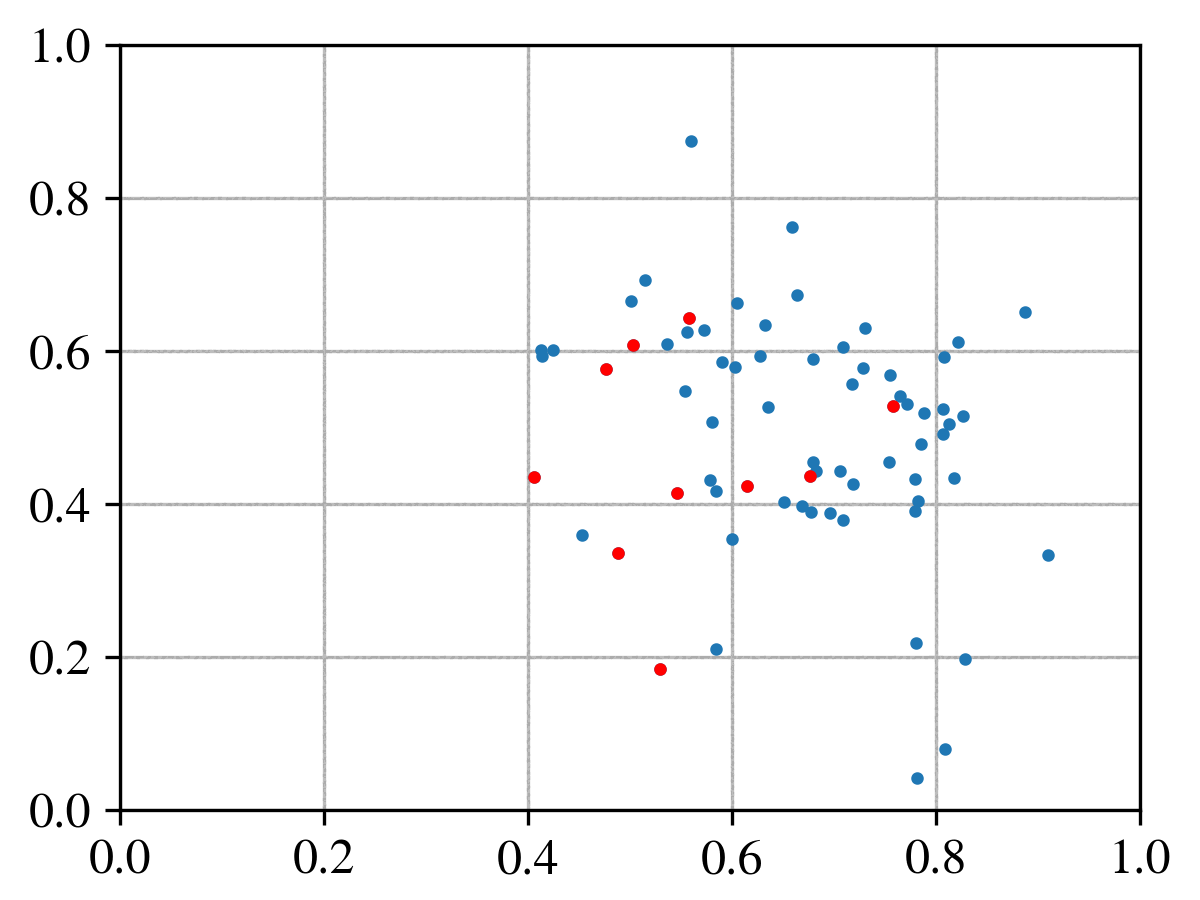
The billiard challenge
Collision of reds against blues
Another day, another test. Here we continue testing the algorithm performance in the collision of particles. This time we analyse the collision of a group of particles (the reds) against the blues. Do we conserve global energy, momentum? How does the particle scattering probability applies in this example? Do we want random isotropic or anisotropic collisions? These were example of questions that we had during this test.
Dark matter halo evolution
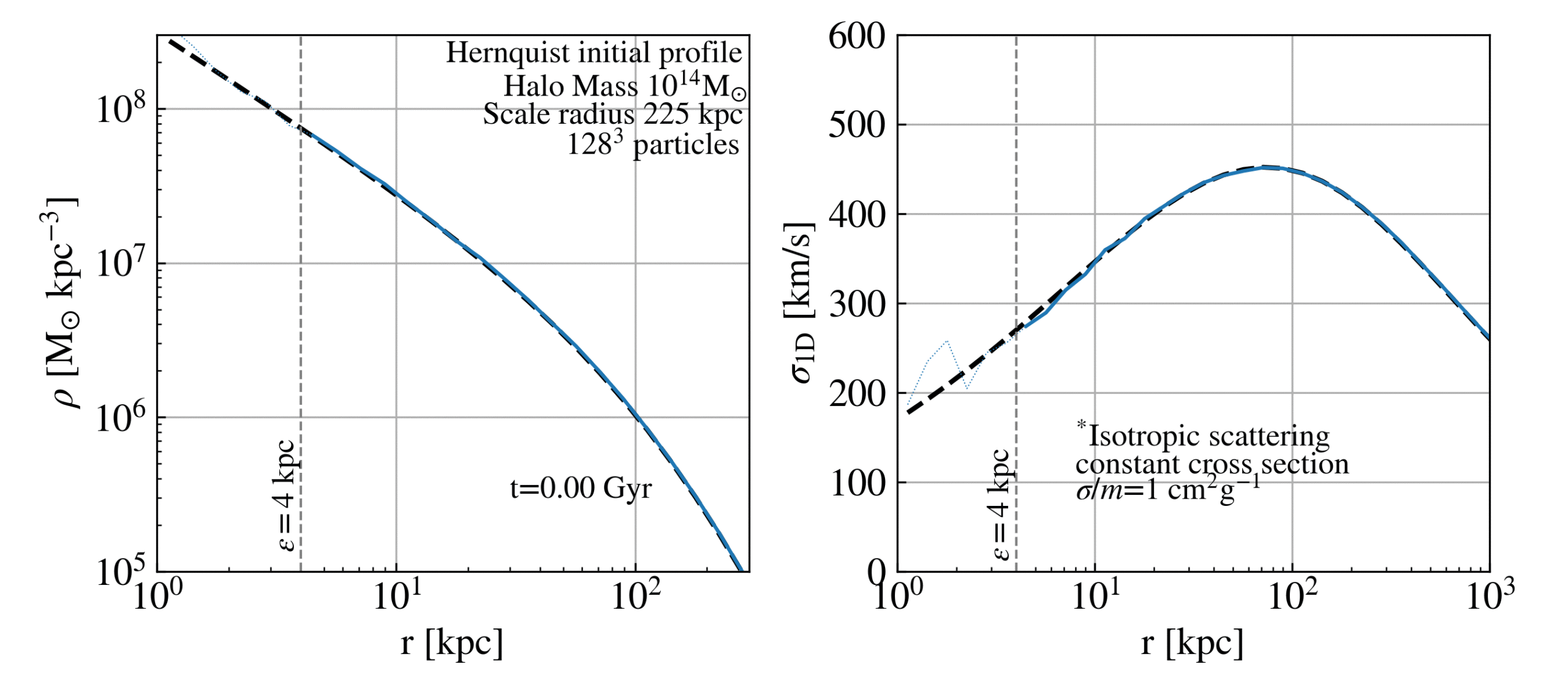
Evolution of a SIDM Hernquist halo
Evolution of the density profile (left panel) and velocity dispersion (right panel) of a 10^14 M⊙ Hernquist halo. The central density rapidly decreases as dark matter particles get hotter due to the repeated collisions. The model is evolved for 10 Gyrs under an isotropic scatter SIDM framework with a constant cross section per unit of dark matter mass of 1 cm^2/g. The halo stabilises with a central constant density (core) and an isothermal velocity dispersion profile.
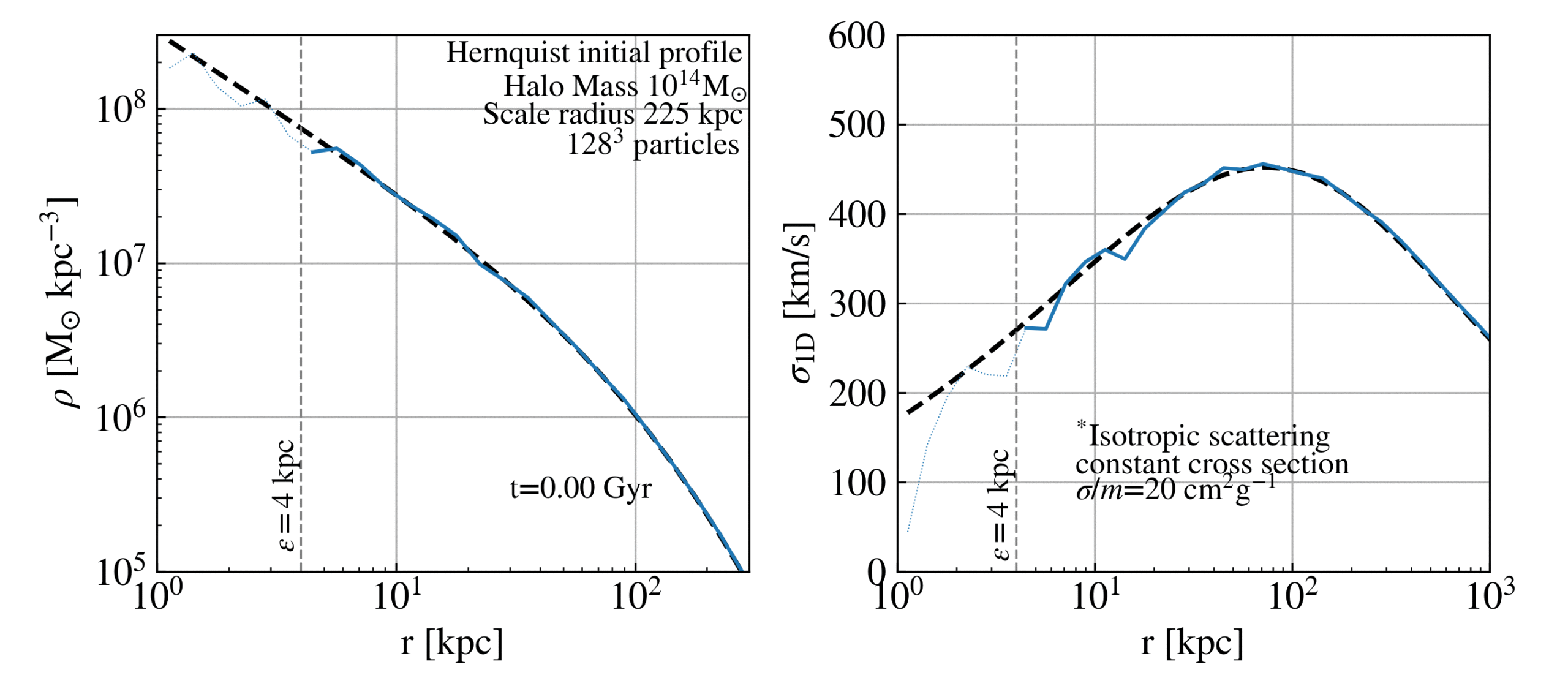
Gravothermal core collapse
Evolution of a Hernquist halo undergoing core-collapse
Similar example as above but in this case the SIDM framework follows isotropic scattering with a constant cross section of 20 cm^2/g. Under this large cross section, the halo becomes rapidly hot with an isothermal profile. This stability period lasts a Gyr, after that the core contraction begins. While maintaining a constant velocity dispersion, the central density raises.